- Cosa sono gli interessi composti?
- A quanto ammontano gli interessi composti
- Piccole nozioni per gli interessi composti
- Differenza tra interessi standard e composti
- Perché sono così importanti gli interessi composti?
Cosa sono gli interessi composti?
Rispondere a questa domanda non è proprio semplicissimo e immediato poiché tutti conoscono l’interesse semplice, che viene menzionato ovunque, che può essere ritirato alla scadenza temporale di un’unità, precedentemente pattuita.
Prima di rispondere a questa domanda bisogna tener presente che gli interessi composti fanno tanta differenza sia in maniera positiva che negativa; detto questo, si può rispondere alla domanda in modo tecnico, affermando che gli interessi composti maturati si aggiungono al capitale iniziale, diventando anch’essi produttivi e si integrano alla quota che genererà gli interessi (gli interessi degli interessi).
A quanto ammontano gli interessi composti
Non è semplice rispondere a questa domanda, ci sono tanti fattori da valutare e da considerare, come le imposte di bollo, la tassazione delle rendite finanziarie etc, che influiscono non di poco sulla somma totale che si ricava dagli interessi e dall’investimento iniziale.
Piccole nozioni per gli interessi composti
Ci sono tre tipi diversi di interessi composti che devono essere considerati:
- Interesse composto discontinuo annuo: in questo caso gli interessi composti sono aggiunti al capitale iniziale che li ha prodotti, una sola volta l’anno in una data prestabilita.
- Interesse composto discontinuo convertibile: in questo caso gli interessi composti sono aggiunti più volte al capitale iniziale che li ha prodotti, anche in questo caso i periodi o le date sono prestabilite.
- Interesse composto continuo: in questo caso si fa riferimento alla matematica finanziaria ed in particolar modo alle applicazioni teoriche, infatti gli interessi composti sono aggiunti al capitale iniziale a ogni istante.
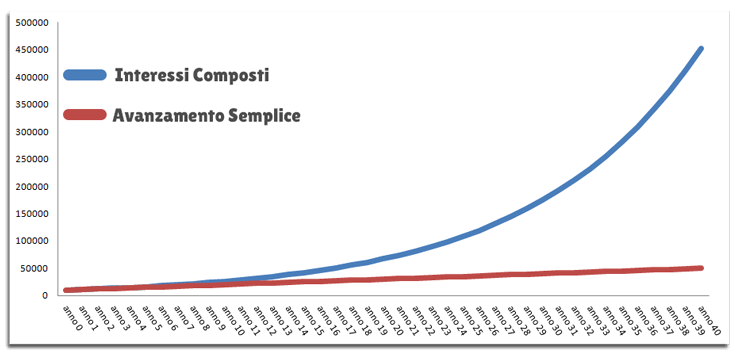
Differenza tra interessi standard e composti
Per rispondere in modo concreto, ma volendo allo stesso tempo essere pratici ed esaustivi, non considerando fattori esterni agli interessi, si può considerare di investire una somma di 10.000 euro e di maturare gli interessi fino al 3% annuo.
A questo punto bisogna fare la differenza tra interessi standard e interessi composti.
Nel primo caso si immaginerà di guadagnare:
- dopo 1 anno di investimento iniziale di 10.000 euro si saranno maturati 300 euro di interessi standard, per un totale di 10.300 euro;
- dopo 10 anni di investimento iniziale di 10.000 euro si saranno maturati 3.000 euro di interessi standard, per un totale di 13.000 euro;
- dopo 20 anni di investimento iniziale di 10.000 euro si saranno maturati 6.000 euro di interessi standard, per un totale di 16.000 euro.
In realtà, con l’interesse composto, si dovranno aggiungere i due tipi di interessi che vengono aggiunti al capitale iniziale, quindi si parlerà di:
- dopo 1 anno di investimento iniziale di 10.000 euro si saranno maturati 300 euro di interessi standard senza interessi composti (non previsti il primo anno), per un totale di 10.300 euro;
- dopo 10 anni di investimento iniziale di 10.000 euro si saranno maturati 3.000 euro di interessi standard e 439 euro di interessi composti per un totale di 13.439 euro;
- dopo 20 anni di investimento iniziale di 10.000 euro si saranno maturati 6.000 euro di interessi standard e 2.061 euro di interessi composti, per un totale di 18.061 euro.
Questa differenza sta nel calcolo non solo degli interessi standard (in questo caso il 3%) ma con l’aggiunta al calcolo degli interessi composti maturati nel tempo, che si sono sommati al capitale iniziale.
Può sembrare molto complicato calcolare gli interessi composti, ma ci si può rifare ad una semplice formula:
IV=CP(1+Y)^X
Dove per IV si intende il valore del proprio investimento dopo X anni, mentre per CP si intende il capitale iniziale, infine per Y si intende la percentuale di interesse standard ^ elevato a potenza.
Per fare un piccolo esempio pratico, bisogna innanzitutto capire che significato ha il tasso di interesse: il tasso di interesse trova il suo pieno significato nel vedersi riconoscere il ritardato utilizzo del capitale.
Esposto questo concetto, che può sembrare totalmente teorico, è riportato un piccolo esempio, per capire quanto inconsciamente si usano i tassi di interesse in qualsiasi occasione:
Simona ha appena preso il suo stipendio ed è intenzionata a spenderli per comprare un mobile per la sua casa. Mentre si reca dal mobiliere, riceve la telefonata di Matteo, che le chiede di prestarle 1.000 euro per delle spese urgenti e impreviste. Simona inizialmente è confusa perché con 1.000 euro comprerebbe il mobile che tanto desiderava; ma alla fine pattuisce con Matteo che quest’ultimo le restituirà i soldi il mese successivo con un interesse del 5%.
Simona ha così deciso di aiutare Matteo, privandosi di acquistare (per quel mese) il mobile tanto agognato. Quando il mese successivo Matteo restituirà a Simona la somma prestata, le darà 1.050 euro. Quindi il fatto di aver ritardato il proprio acquisto ha permesso a Simona di comprare il mobile desiderato, ma di avere anche 50 euro in più che utilizzerà per un’uscita in più con la sua amica.
Morale della favola, il riconoscimento del ritardato utilizzo ha permesso a Simona di guadagnare un’extra.
A questo esempio possiamo tranquillamente aggiungere gli interessi composti:
Supponiamo che Matteo, dopo aver restituito i soldi a Simona, la richiama per farsi riprestare la stessa cifra ed in più chiede di inserire i 50 euro degli interessi sul capitale da prestargli per le sue spese. Tanto alla fine restituirà tutto insieme.
Alla fine del brutto periodo, Matteo ripaga Simona restituendole una somma pari a 1.102,50 euro. Improvvisamente si notano 2,50 euro che ‘’sarebbero difficili da comprendere’’, se non fosse per il fatto che i 2,50 fanno parte del 5% di interessi composti. Quindi, per aver prestato dei soldi a Matteo, Simona non solo ha guadagnato 100 euro di interessi semplici, ma 2,50 euro di interessi composti che potrà utilizzare per un caffè al bar in compagnia.
Perché sono così importanti gli interessi composti?
Per prima cosa, capire la differenza tra interessi semplici e composti è fondamentale per evitare spiacevoli equivoci o addirittura può evitare qualche bella fregatura.
Infatti, quando in un investimento si parla di interessi composti, si sta parlando di un valore aggiunto, lo stesso vale quando si chiede un prestito o un mutuo; in questo caso gli interessi composti sono svantaggiosi perché ci si trova a dover restituire davvero una somma alquanto diversa da quella che ci si aspettava, quelli che in gergo vengono chiamati gli interessi degli interessi. Quindi meglio pensare agli interessi composti solo in maniera positiva.
Si possono considerare gli investimenti composti un vero affare?
Certo che si può, ma sempre non considerando le tasse, i bolli, i rischi o l’impatto dell’inflazione. Difatti, sempre nel mondo ideale, gli interessi composti sono una specie di rendimento extra che si può avere da un investimento iniziale. Molto importante, a questo punto, è capire che tipo di investimento si voglia fare; infatti, maggiori guadagni si hanno lasciando depositati i soldi per tanto tempo, visto che gli interessi composti si aggiungono all’investimento iniziale e sono col tempo ricapitalizzati.
In altre parole, una piccola somma investita, può sul lungo periodo diventare una somma molto cospicua.
È quindi chiaro che il fattore tempo è un coprotagonista quando si tratta di interessi composti. È come prepararsi per un lungo viaggio, più saranno gli accorgimenti e le strategie da adottare, più semplice e sereno sarà il cammino per raggiungere la propria meta.
Del resto Albert Einstein ha definito l’interesse composto l’ottava meraviglia del mondo, poiché secondo lui era stata la scoperta matematica migliore di tutti i tempi.
Articoli correlati:
Politiche agricole: il divario fra Nord e Sud del mondo al WTO di Cancùn
La new economy e la crisi del capitale, mondo del lavoro e capitalismo
Enpap: previdenza psicologi, info complete
Coinspace Truffa? Info opinioni e recensioni
GoldBet scomesse, truffa o no?
Investire in derivati: opzioni, futures, azioni, swaps
Postepay, info utili
Prestito Personale
